Proton Momentum: Hiding in Plain Sight?
By Adam Green
Protons at first glance seem like simple objects. They have well-defined spin (+1/2) and electric charge (-1), and we even know their quark compositions. A proton is composed of two up quarks and one down quark. If a proton is moving, it also carries a reasonably well-defined momentum. How is this momentum distributed between the constituent quarks? Intuitively, it seems like the momentum should be evenly distributed between the quarks, each carrying 1/3 the total momentum. It turns out that this is not the case.
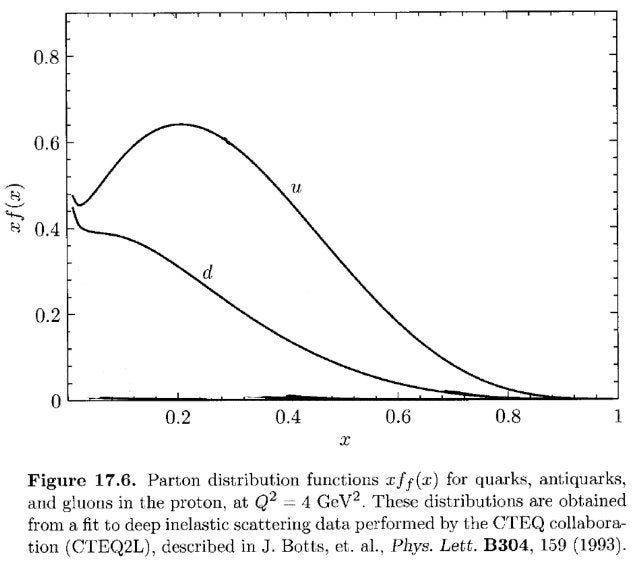
Below is a plot of the momentum distribution of the up and down quarks inside a proton, adapted Peskin and Schroeder, An Introduction to Quantum Field Theory. Some data is omitted to illustrate a point.
On the horizontal axis is the momentum fraction, x. A momentum fraction of 1 means that the quark carries 100% of the proton momentum. A momentum fraction of 0 means that the quark carries none of the proton momentum. On the vertical axis, we have the probability to find a quark with that particular momentum fraction, xf(x). For a given momentum fraction x, if xf(x) is large then we are very likely to observe a quark with momentum fraction x. The curves are labeled u and d for up and down quarks respectively. We are 60% likely to see an up quark carrying 20% of the proton momentum, and 20% likely to see a down quark carrying 40% of the proton momentum.
From conservation of momentum, the laws of physics require that the total momentum of the quarks add up to the momentum of the proton. If we compute the total momentum of the quarks, by computing the area under each curve, we find that the up quarks carry only 36% of the total momentum, and the down quarks carry only 18% of the total momentum! Clearly these two don’t add up to 100%, so there must be more going on that we are missing.
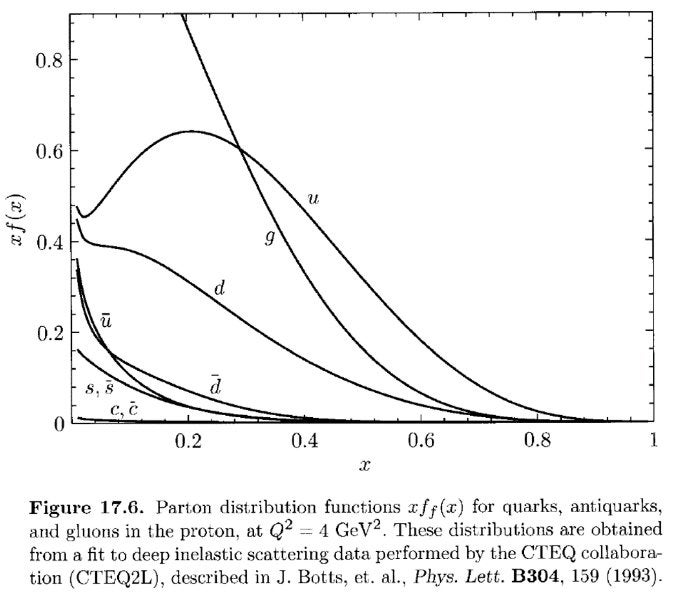
It turns out that in addition to 2 ups and 1 down, protons are also made of antiquarks, and gluons! The full momentum distribution of a proton is given below.
Now, we have seven more curves in addition to the original u and d curves, representing seven more particles! The curve labeled g stands for gluons. These are the particles that transmit the strong nuclear force. It is this force that is responsible for holding quarks together to even form protons. The c and s curves stand for Charm and Strange quarks. Finally, curves labeled with a bar denote antiquarks.
From this plot, we are forced to conclude that protons are much more complex than 2 up quarks and 1 down quark. To be precise, we would say that these quarks are the “valence” quarks of the proton, just like valence electrons of atoms. These valence quarks are the quarks that are available to interact with other particles.
Reference
Peskin and Schroeder, An Introduction to Quantum Field Theory, Section 17.4, figure 17.6.